New Approach of Civil Age Estimation Based on the Study of Permanent Teeth Eruption
A B S T R A C T
Civil age estimation is part of the process of individual identification for judicial purpose. It must be applicable for dead bodies as well as for living persons. Age can be estimated through the analysis of the permanent teeth eruption process. In the present study, this process was analysed based on the Bengston’s revisited stages illustrated by AlQhatani et al. in 2010. They were used to build a linear regression model for age estimation of children. This model was built on a sample composed of 191 orthopantomographs of children aged from 9 to 19.9 years old. The created model allowed the elaboration of a formula for civil age estimation based on the most relevant teeth groups associated to their eruption stages. The estimated age showed a good correlation with civil age (R2: 0.74), and a good accuracy rate (57% at +/- 12 months and 75% at +/- 18 months). Despite what was expected, sex was not correlated with age and was discarded from the analysis.
Keywords
Age estimation, dental eruption, orthodontia, anthropology, odontology
Introduction
Age estimation can find application in several disciplines such as anthropology, odontology, and forensic sciences. In the anthropology field, this estimation can be made by bony and/or dental elements of the remains. However, teeth are an element of choice whenever they are available due to their better conservation throughout time, thanks to their position enclaved in the mouth [1]. Age estimation appears to have a crucial importance in the French forensic field, as different procedures may be intended depending on the age of the defendant. Key ages are 13, 16 and 18 years old in French law [2]. In adult population, different criteria are available for age determination: tooth wear, root dentine transparency and apposition of secondary dentine [3]. New methods based on pulp-tooth ratio have been recently developed using three-dimensional imaging [4-6]. When age estimation concerns immatures, two principal events can be used: tooth development or tooth eruption. The term of eruption used here is defined as: “… a developmental process during which the tooth moves vertically from its initial position in the alveolar crypt to its functional position in the occlusal plane. During this ongoing process, one particular step is constituted by dental emergence” [7]. In humans, teeth are develop following a specific process. Four stages can be identified: calcification initiation, crow completion, eruption and finally, root completion [8].
The interest of using eruption stage for age determination is its applicability on dry bone or medical images. Several studies were conducted based on the different stages of dental development. The best known are the method of Nolla et al. and the method of Demirjian et al., which was revisited in 1980 to take into consideration the sex variable [9-11]. This new parameter holds a strong importance because a notable dimorphism starts at the stage of tooth crown completion. Thus, for age estimation of immatures, it is important to distinguish sexes which do not evolve simultaneously, as it could influence the reliability of the results. Even though Demirjian’s method is well known and used, it is important to notice that it is not applicable on all populations. Indeed, Willems et al. highlighted an overestimation of age when applied on an European population [12]. The objective of the present study was to create an age estimation formula for immature subjects, based on the eruption stage of permanent teeth. We focused on the permanent teeth eruption Bengston’s stages (1935) stages as revised by AlQhatani et al. in 2010 [13]. It shows the 4 positions of an erupting tooth:
i. Occlusal or incisal surface is covered entirely by bone.
ii. Occlusal or incisal surface breaks through the crest of the alveolar bone.
iii. Occlusal or incisal surface is midway between the alveolar bone and the occlusal plane.
iv. Occlusal or incisal surface is in the occlusal plane.
Materials and Methods
I Materials
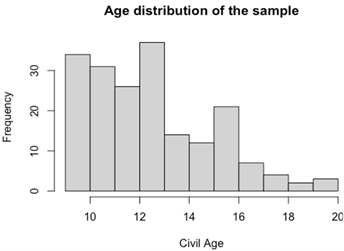
A total of 191 orthopantomographs were retrospectively collected from the dento-facial odontology department of the hospital of La Timone, in Marseille, France. The X-rays were conducted between 2014 and 2020. To be included in the study, individuals should not present any history of orthodontic treatment or dental agenesis. To ensure the confidentiality of the patients, all the data were anonymized. The study was reviewed and approved by the RGPD (Règlement Général européen de Protection des Données, n°2021-16). The sample was composed of subjects aged from 9 to 19.9 years old and were selected from a multi-ethnic population. The sample was composed of 101 girls and 90 boys, with a mean age of 12.63 years old (Table 1, Figure 1). Regarding the third molars, agenesis would be considered if one of the 4 wisdom teeth was missing above the age of 13 years old [14].
Figure 1: Distribution of the 191 individuals of the sample depending on age (in years).
Table 1: Description of the sample. Number of subjects and mean
age (in years) by sex and for the total sample.
|
Sample |
Number of subjects |
Mean reel age (Years) |
|
Females |
101 |
12.48 |
|
Males |
90 |
12.80 |
|
Total |
191 |
12.63 |
i Statistical Analysis
All statistical analyses were performed using RStudio software (4.0.5). Significance threshold was set to 0.05 for all tests. First, a Shapiro-Wilk test did not assess the normality of the data distribution.
Thus, non-parametric tests were used considering the discreet nature of the variables. The data were submitted to a correlation analysis of Spearman: to determine how much the variables were related to the civil age. To evaluate the method reproducibility, a random set of 30 orthopantomographs, extracted from the original sample, was examined by a second observer from the same academic level. Information such as age or sex were hidden from the observer. The repeatability was also tested on the same 30 orthopantomographs. Reliability was assessed based on the precision (residuals) and fidelity (repeatability and reproducibility) of age estimation. Both the inter and intra-observers analysis were performed using the Concordance Correlation Coefficient (CCC) of Lin. Partik et al. proposed an interpretation of the CCC results, which was used in this study [15].
ii Linear Regression Analysis
A multiple linear regression analysis was performed to build a formula for age estimation civil age based on the teeth eruption stages. Firstly, the most relevant variables were selected by a stepwise selection method. Only the most significant and non-collinear variables were retained to build the model. The regression model was built with the most relevant teeth groups and stages based on the power coefficient of the correlation (adjusted R²) and the p-value resulting from the stepwise regression analysis (<0.05). The mean absolute error of the estimation was then assessed. An analysis of the residuals was performed to appreciate the precision of the formula: by evaluating the proportion of individuals whose estimated age lied between +/-12 months or +/-18 months (estimation considered, respectively, as precise, or acceptable). Residuals were defined as the value of the difference between civil age and estimated age.
Results
The correlation coefficients obtained with the Spearman method are presented in (Table 2). The maximum was identified for molars at stage 4 (M_St4) with a correlation coefficient (CC) of 0.79; the less correlated variable was molars at stage 3 (CC: - 0.04). Mean CC value is -0.03. The correlation was considered as good if | CC | >0.60 and excellent if | CC | > 0.75. The implication of sex in the age estimation was tested both with the correlation and the linear regression. It was found that this variable was not significantly correlated (CC: -0.05) and was consequently discarded from the study. The most relevant teeth groups and stages selected by the regression model were the number of premolars at stage 4 (PM_St4), and the number of molars at stage 1 (M_St1) and at stage 4 (M_St4). Finally, age can be estimated according to the following formula:
\[Age=PM_{St4}\ast0.17882\ -M_{St1}\ast\ 0.47256\ +M_{St4}\ast0.55301\ +10.24844\]The formula’s precision rate was appreciated with the analysis of the residuals of the regression model: see (Figure 2) and (Table 3). The selected model was shown to estimate 57% (n=110) of the individuals’ age between +/- 12 months of age and 75% (n=144) between +/- 18 months, which can be considered as a good precision rate.
Table 2: Description of the variables and their correlation
coefficient with reel age.
|
Variables |
Correlation coefficient
(Spearman) |
P-value |
|
I_St1 |
-0.135148 |
0.06231 |
|
I_St2 |
-0.2141245 |
0.002936 |
|
I_St3 |
-0.2470138 |
0.0005712 |
|
I_St4 |
0.2727233 |
0.0001351 |
|
C_St1 |
-0.6170941 |
<
2.2e-16 |
|
C_St2 |
-0.3976513 |
1.225e-08 |
|
C_St3 |
0.7395386 |
<
2.2e-16 |
|
C_St4 |
0.7395386 |
<
2.2e-16 |
|
PM_St1 |
-0.6801941 |
<
2.2e-16 |
|
PM_St2 |
-0.4880747 |
7.956e-13 |
|
PM_St3 |
-0.3425723 |
1.229e-06 |
|
PM_St4 |
0.7607081 |
<
2.2e-16 |
|
M_St1 |
-0.6856221 |
<
2.2e-16 |
|
M_St2 |
-0.2358707 |
0.00102 |
|
M_St3 |
-0.04920808 |
0.499 |
|
M_St4 |
0.7981866 |
<
2.2e-16 |
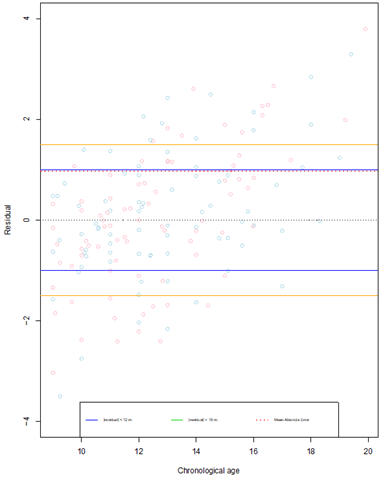
Figure 2: Scatterplot of the residuals’ dispersion associated to the regression model according to chronological age (in years). The lines (blue and orange) overlines the +/- 12 months and +/- 18 months respectively. The red pointed line represents the Mean Absolute Error.
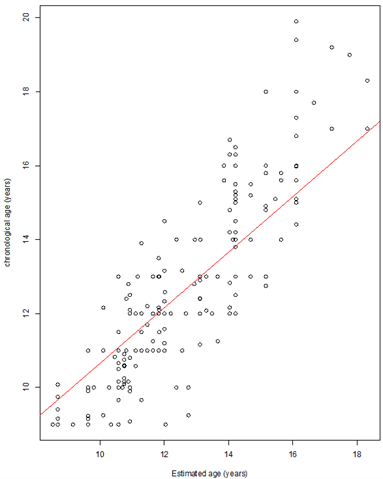
Overestimation of age was assessed when residuals were negative. Thus, 56% of the estimated ages were overestimated (n=108). The mean absolute error between reel age and estimated age was 11.52 months (confidence interval at 95% in months: -2.04 – 2.04). Inter- and intra-observers analysis showed a good repeatability (CCC: 0.79) and reproducibility (CCC: 0.75). Table 3 presents the percentage of precision of age estimation for each age class. As it is observed on the graphical representation of the residuals (Figure 2), this precision decreased between 9 to 14 years old (for +/- 12 months, the precision rate decreased from 91% to 20%). Between 14 and 16 years old, there was an augmentation before a new diminution after 16 years old. However, it should be noted that the lower precision groups were also composed by the lower number of individuals ((13-14); (6-17); (17-19), each group was composed of 5 subjects). To compare the results with the perfect linear relation between chronological and estimated age, a regression line was added to the graph (Figure 3). Regarding the evaluation of the repeatability and reproducibility of the method, the CCC were, respectively, of 0.79 and 0.75.
Table 3: Precision of age estimation and overestimation by age
group. Two groups of age (17-18 and 18-19) were reunited because of the low
number of individuals.
|
Age group (years) |
Size (n) |
Precision at +/- 12 months (%) |
Precision at +/- 18 months (%) |
Over-estimation (%) |
|
(9-10) |
12 |
91 |
91 |
66 |
|
(10-11) |
15 |
66 |
100 |
6 |
|
(11-12) |
9 |
55 |
66 |
33 |
|
(12-13) |
19 |
42 |
52 |
47 |
|
(13-14) |
5 |
20 |
40 |
20 |
|
(14-15) |
8 |
87 |
87 |
75 |
|
(15-16) |
14 |
92 |
100 |
7 |
|
(16-17) |
5 |
0 |
20 |
0 |
|
(17-19) |
5 |
20 |
20 |
20 |
Figure 3: Plot of chronological age against estimated age of the individuals composing the sample.
Discussion
Age estimation in anthropology is a central element for the constitution of a biological profile which is crucial for the identification of osteological remains [16]. Furthermore, teeth are frequently in a better preservation state than bony elements of the skeleton. Age estimation can also be applied to living individuals. For instance, age determination is important for practitioners of odontology in terms of development disorders assessment and treatment planning [17]. In European countries, migration led to new application of age estimation methods on living people who do not possess reliable identity documents. This applicability on living individuals justifies the need of a method rapidly realizable and the least invasive. In this objective, the choice of a method based on X-rays is the most relevant. The civil age of an individual is estimated from an assessment of a physiological age [18]. In this case, dental age was assessed by the study of a specific process, the permanent teeth eruption. This process is a short period phenomenon, occurring in the young years of our lives. The tooth moves from its original position into the bone, to its occlusive position in the mouth. The aim of the present study was to use this process of permanent teeth eruption to establish a new method to estimate non-adults’ age.
Surprisingly, sex was not correlated with age. The opposite was expected because of the numerous studies indicating the advance of girls over boys, especially in the puberty ages [10, 19]. The calculation of age was based on two teeth groups: premolars (PM_St4), and molars (M_St1 and M_St4). The linear regression analysis demonstrated a decrease in precision linked with age. This could be explained by the reduction of discriminant factors considering teeth eruption in the older age groups. Indeed, the more aged individuals have normally achieved all their teeth eruption (stage 4), except for the third molar. Furthermore, as it was mentioned previously in the literature, for adolescents, age estimation shows a lower precision with radiological method, but it remains the most accurate method for this group of age [20]. This decrease in precision could also, or in addition, be explained by the smaller number of individuals in the considered groups (16-17 and 17-19). From the perspective of improvement of this study, it would be necessary to include more individuals aged between 16 and 19 years old. The statistical analysis demonstrated the satisfactory reliability of the method, based on the CCC criterion. Partik et al. in 2002 proposed an interpretation of the concordance coefficient, between 0.71 and 0.80, it can be considered as satisfactory [15]. Here, the concordance coefficients were 0.75 and 0.79 for respectively, reproducibility and repeatability. However, this reliability could be improved by a larger sample including individuals less at risk of presenting eruptive failures.
Indeed, the main limitation of this study was the sample composition: the X-rays used for the analysis were collected from a population consulting for orthodontic treatment. Teeth eruption failure can be caused by an obstruction of the eruption pathway or by other disorders that could have impacted the well development and/or eruption of the teeth. Furthermore, some systemic or syndromic cause can affect teeth eruption. Hanisch et al. made a list of those rare pathologies that were linked to an eruption failure [21]. To prevent for those cases, all subject presenting agenesis of one or more teeth were excluded from the sample. Nevertheless, the population used to collect the sample was multi-ethnic, which is an advantage for the development of a method. Indeed, this makes the age estimation formula applicable to different populations, as it was described that ethnicity can affect the teeth eruption process [22]. It was previously determined in the literature that the eruption process is linked with the root development [23]. An interesting question to ask is, does a method based on teeth eruption can have comparable results with a method based on the root development? Cameriere et al. developed an age-estimation formula based on the measurements of open apices [24]. Its comparison with the present results would be interesting to go further in the investigations. Also, to apply our method based on teeth eruption on ancient dental remains would allow to test its applicability for bioarcheological context. Moreover, confronting this work to other osteological age estimation methods would provide more information on the contribution of stages implemented to this regression model, compared to other method based on teeth eruption [12].
Conclusion
The created model allowed the elaboration of a formula for civil age estimation based on the most relevant teeth groups associated to their eruption stages. The estimated age showed a good correlation with civil age (R2: 0.74), and a good accuracy rate (57% at +/- 12 months and 75% at +/- 18 months). Despite what was expected, sex was not correlated with age and was discarded from the analysis.
Funding
None.
Conflicts of Interest
None.
Article Info
Article Type
Research ArticlePublication history
Received: Thu 20, Jan 2022Accepted: Wed 09, Feb 2022
Published: Mon 28, Feb 2022
Copyright
© 2023 Camille Philip-Alliez. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Hosting by Science Repository.DOI: 10.31487/j.DOBCR.2022.01.01
Author Info
Camille Philip-Alliez Michel Le Gall Adele Brotons Oceane Monachini Bruno Foti Floriane Remy
Corresponding Author
Camille Philip-AlliezMCU-PH Orthopedie Dento-Faciale, Hopital de La Timone, Marseille, France
Figures & Tables
Table 1: Description of the sample. Number of subjects and mean
age (in years) by sex and for the total sample.
|
Sample |
Number of subjects |
Mean reel age (Years) |
|
Females |
101 |
12.48 |
|
Males |
90 |
12.80 |
|
Total |
191 |
12.63 |
Table 2: Description of the variables and their correlation
coefficient with reel age.
|
Variables |
Correlation coefficient
(Spearman) |
P-value |
|
I_St1 |
-0.135148 |
0.06231 |
|
I_St2 |
-0.2141245 |
0.002936 |
|
I_St3 |
-0.2470138 |
0.0005712 |
|
I_St4 |
0.2727233 |
0.0001351 |
|
C_St1 |
-0.6170941 |
<
2.2e-16 |
|
C_St2 |
-0.3976513 |
1.225e-08 |
|
C_St3 |
0.7395386 |
<
2.2e-16 |
|
C_St4 |
0.7395386 |
<
2.2e-16 |
|
PM_St1 |
-0.6801941 |
<
2.2e-16 |
|
PM_St2 |
-0.4880747 |
7.956e-13 |
|
PM_St3 |
-0.3425723 |
1.229e-06 |
|
PM_St4 |
0.7607081 |
<
2.2e-16 |
|
M_St1 |
-0.6856221 |
<
2.2e-16 |
|
M_St2 |
-0.2358707 |
0.00102 |
|
M_St3 |
-0.04920808 |
0.499 |
|
M_St4 |
0.7981866 |
<
2.2e-16 |
Table 3: Precision of age estimation and overestimation by age
group. Two groups of age (17-18 and 18-19) were reunited because of the low
number of individuals.
|
Age group (years) |
Size (n) |
Precision at +/- 12 months (%) |
Precision at +/- 18 months (%) |
Over-estimation (%) |
|
(9-10) |
12 |
91 |
91 |
66 |
|
(10-11) |
15 |
66 |
100 |
6 |
|
(11-12) |
9 |
55 |
66 |
33 |
|
(12-13) |
19 |
42 |
52 |
47 |
|
(13-14) |
5 |
20 |
40 |
20 |
|
(14-15) |
8 |
87 |
87 |
75 |
|
(15-16) |
14 |
92 |
100 |
7 |
|
(16-17) |
5 |
0 |
20 |
0 |
|
(17-19) |
5 |
20 |
20 |
20 |
References
1.
Shah P, Velani PR,
Lakade L, Dukle S (2019) Teeth in forensics: A review. Indian J Dent Res
30: 291-299. [Crossref]
2.
Ordonnance n°45-174
du 2 fevrier 1945 relative à l’enfance délinquante articles 7,15, 20 et code
civil art. 1240 à 1244, n.d.
3.
Cameriere R, Ferrante
L, Belcastro MG, Bonfiglioli B, Rastelli E et al. (2007) Age estimation by pulp/tooth ratio in canines by mesial and
vestibular peri-apical X-Rays. J Forensic Sci 52: 1151-1155. [Crossref]
4.
Tardivo D, Sastre J,
Catherine JH, Leonetti G, Adalian P et al. (2014) Age determination of adult individuals by three-dimensional
modelling of canines. Int J Legal Med 128: 161-169. [Crossref]
5.
Kazmi S, Mânica S,
Revie G, Shepherd S, Hector M (2019) Age estimation using canine pulp volumes
in adults: a CBCT image analysis. Int J Legal Med 133: 1967-1976. [Crossref]
6.
Colombo A,
Coqueugniot H, Dutailly B, Desbarats P, Tillier AM (2013) Nouvelles données sur
l’édification des molaires et l’estimation de l’âge dentaire des enfants par
imagerie médicale et 3D: apports et perspectives. Bull Mém Soc Anthropol
25: 127-146.
7.
Heuzé Y (2004)
Chronologie et étiologie de la maturation macrostructurale des dents
définitves. Univ Sci Et Tech Bord.
8.
Nolla CM (1960) The
development of permanent teeth. J Denst Child 27: 254-266.
9.
Demirjian A, Goldstein
H, Tanner JM (1973) A new system of dental age assessment. Hum Biol 45:
211-227. [Crossref]
10.
Demirjian A,
Levesque GY (1980) Sexual differences in dental development and prediction of
emergence. J Dent Res 59: 1110-1122. [Crossref]
11.
Willems G, Van
Olmen A, Spiessens B, Carels C (2001) Dental age estimation in Belgian
children: Demirjian’s technique revisited. J Forensic Sci 46: 893-895. [Crossref]
12.
Foti B, Adalian P,
Lalys L, Chaillet N, Leonetti G et al. (2003) [Probabilistic approach to age
estimation of children by dental maturation]. C R Biol 326: 441-448. [Crossref]
13.
AlQahtani SJ,
Hector MP, Liversidge HM (2010) Brief communication: The London atlas of human
tooth development and eruption. Am J Phys Anthropol 142: 481-490. [Crossref]
14.
Chourbaji C (2016)
Troisièmes molaires: conserver ou extraire? Critères de décisions. Sci Viv.
15.
Partik BL, Stadler
A, Schamp S, Koller A, Voracek M et al. (2002) 3D versus 2D ultrasound:
accuracy of volume measurement in human cadaver kidneys. Invest Radiol
37: 489-495. [Crossref]
16.
Christensen AM,
Passalacqua NV, Bartelink EJ (2014) Age Estimation in: Forensic Anthropology. Elsev
243-284.
17.
Kirschneck C, Proff
P (2018) Age assessment in orthodontics and general dentistry. Quintessence
Int 49: 313-323. [Crossref]
18.
Age Estimation.
(2013) Sci Wor Gro Fore Anth (SWGANTH).
19.
Levesque GY,
Demirjian A, Tanguay R (1981) Sexual dimorphism in the development, emergence
and agenesis of the mandibular third molar. J Dent Res 60: 1735-1741. [Crossref]
20.
Ritz Timme S,
Cattaneo C, Collins MJ, Waite ER, Schütz HW et al. (2000) Age estimation: the
state of the art in relation to the specific demands of forensic practise. Int
J Legal Med 113: 129-136. [Crossref]
21.
Hanisch M, Hanisch
L, Kleinheinz J, Jung S (2018) Primary failure of eruption (PFE): a systematic
review. Head Face Med 14: 5. [Crossref]
22.
Olze A, van Niekerk
P, Ishikawa T, Zhu BL, Schulz R et al. (2007) Comparative study on the effect
of ethnicity on wisdom tooth eruption. Int J Legal Med 121: 445-448. [Crossref]
23. Nagata M, Ono N, Ono W (2020) Mesenchymal Progenitor Regulation of Tooth Eruption: A View from PTHrP. J Dent Res 99: 133-142. [Crossref]
24. Cameriere R, Ferrante L, Cingolani M (2006) Age estimation in children by measurement of open apices in teeth. Int J Legal Med 120: 49-52. [Crossref]
